Thomas' Labs | Fast Fourier Transform

In this article I attept to explain the principles of the fast fourier transform (FFT) and develop in incremental steps an implementation in common lisp.

NOTE: This is part of my personal notes and as such may contain mistakes or not be correct at all. If you find any issues please contact me at my email address.

Introduction

The FFT is an algorithm for computing the discrete fourier transform (DFT) of an array of values that is meant to be faster than the usual naive implementation. Instead of having the usual behaviour it is an algorithm.

Derivation

To derive the FFT we first consider the definition of the DFT

Let be an array of N, possible complex, numbers such that for some integer . The DFT of is an array of the same length defined as:

A possible implementation of this in code would be something like the following:

(defun dft (x)
  "Naive discrete fourier transform, not fft"
  (flet ((transform (k)
           (loop :with i = (complex 0 1)
                 :for n :below (length x)
                 :sum (* (aref x n) (exp (- (/ (* 2 pi i k n) (length x))))))))
    (map-seq-iota #'transform (length x))))

But we can do a lot better in terms of performance. To this end we first split the sum into even and odd members

Where and themselves are FFTs of a smaller array each. Furthermore notice how thanks to the cyclic nature of the complex exponential function it is possible to half the number of computations:

Thus

Implementing the FFT

With the reduction identities we derived for the FFT a preliminary implementation could be:

(defun fft (sequence)
  (labels
      ((fft-step (n step offset)
         (let ((ret (make-array n)))
           (if (= n 1)
               (setf (aref ret 0) (aref sequence offset))
               (loop
                 :with n2 = (/ n 2)
                 :with ek = (fft-step n2 (* 2 step) offset)
                 :with ok = (fft-step n2 (* 2 step) (+ offset step))
                 :for k :below n2
                 :for c = (exp (- (/ (* 2 pi (complex 0 1) k) n)))
                 :do
                    (setf (aref ret k) (+ (aref ek k) (* c (aref ok k)))
                          (aref ret (+ k n2)) (- (aref ek k) (* c (aref ok k))))))
           ret)))
    (fft-step (length sequence) 1 0)))

The function fft-step needs to be able to access both even and odd terms, for this we use the step and offset arguments. step indicate the distance between consecutive elements of the input to the fft. If we wanted to compute the FFT of the even terms, this distance would be 2. For the fft inside this outer fft of the even entries we also want to split further into even an odd members, this step needs to be 4 and so on. offset represents how many elements must be skipped until the first element of the subarray.

Notice that we are allocating in each step a new array to return. The FFT can however be computed with a single array allocation. For that we store the values of in the first half of the return array and the values of in the second half. Finally we use the so called "butterfly" operations to compute the final result.

Figure 1: Diagram of the abstract data flow inside the FFT. Observe how the FFT itself is define recursively halving the number of items in each step

(defun fft* (sequence)
  (let ((result (make-array (length sequence))))
    (labels ((fft-step (n step offset roffset)
               (if (= n 1)
                   (setf (aref result roffset) (aref sequence offset))
                   (let ((n2 (/ n 2)))
                     (fft-step n2 (* 2 step) offset roffset)                 ; e_k
                     (fft-step n2 (* 2 step) (+ offset step) (+ roffset n2)) ; o_k
                     (loop :for k :below n2
                           :for j = (+ roffset k)
                           :for c = (exp (- (/ (* 2 pi (complex 0d0 1d0) k) n)))
                           :for ek = (aref result j)
                           :for ok = (aref result (+ j n2))
                           :do
                              (setf (aref result j)        (+ ek (* c ok))
                                    (aref result (+ j n2)) (- ek (* c ok))))))))
      (fft-step (length sequence) 1 0 0)
      result)))

fft* is still a recursive function and as such the call stack will grow as . As a last step let us introduce a last iterative version of our function.

(defun fft (sequence)
  (flet ((reverse-bits (bits n)
           (loop :for k :below n
                 :summing (if (logbitp k bits)
                              (ash 1 (- n k 1))
                              0))))
    (let* ((n (length sequence))
           (result (make-array n))
           (nbits (logcount (1- n))))
      (dotimes (i n)
        (setf (aref result i) (aref sequence (reverse-bits i nbits))))
      (do ((q 1 (1+ q)))
          ((>= q (1+ nbits)))
        (let ((b (ash 1 (1- q))))
          (dotimes (i (ash n (- q)))
            (dotimes (j b)
              (let ((even (aref result (+ (ash i q) j)))
                    (odd (aref result (+ (ash i q) j b)))
                    (c (exp (- (/ (* 2 pi (complex 0 1) j) (* b 2))))))
                (setf (aref result (+ (ash i q) j)) (+ even (* c odd)))
                (setf (aref result (+ (ash i q) j b)) (- even (* c odd))))))))
      result)))

reverse-bits is responsible for reordering the initial array the same way the deepest call of fft-step in the recursive version would.

There are still many optimizations that could be made to speed up our code, like twiddle factors, cache optimizations, further prime factors and many others. But this goes beyond the scope I planned for this article. Many would probably be also beyond the scope of my current abilities.

Asymptotic performance

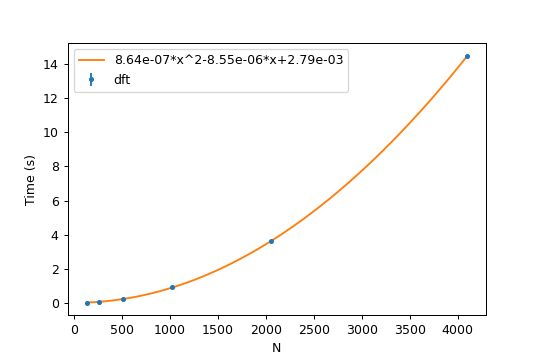
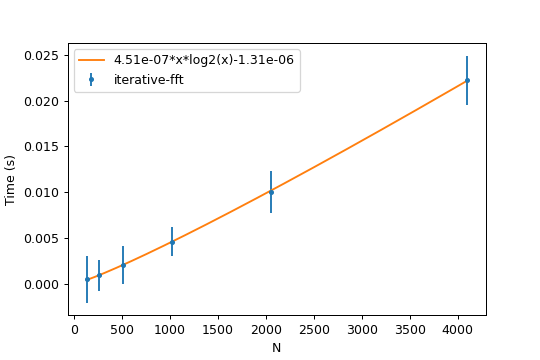
Thoughout this article I claimed that the performance of the FFT scales like instead of the usual performance of the naive DFT. While this can be proven by analizing the provided source code, I decided to run some meassurements and compare them with their respective big-O functions.